Revised March 30, 2019.

• How high can the child count (without assistance)?  Find out how high the child can count on her own, by saying: "Please count as high as you can.”  If the child stops, prompt by asking, “And then comes?” See how high the child can count without making an error. That is a baseline for how high the child can count right now.  Watch Ben: Count Sequence here.
• How high can the child count (with some assistance)? Find out how high the child can count, by saying:  "Please count as high as you can.”  If the child stops and does not know how to continue, say the next number. See if the child can continue from there. Children may be especially likely to stop before reaching the next tens number, for example, saying “36, 37, 38, 39…” and then stopping at 39. If the child is stuck, offer assistance (saying “40” or answering any questions the child asks) to see if the child can continue.  Watch Anna: Count Sequence here.
• Knowledge of the count sequence.  Find out how well the child knows the count sequence, by giving a number out of sequence and asking what comes next. For example, without counting up to 3, say, “What number comes after 3?” For older children, try higher numbers. “What number comes after 16? after 29? after 41?”  If the child has a firm grasp on the count sequence, ask about numbers that come before. For example, “What number comes before 6?” In general, asking children to count backward to find what comes before is more challenging for them than asking what comes next.
• Catch my mistake. Find out how well the child knows the count sequence by making a deliberate mistake. Say, “I’m going to count. You tell me if I make any mistakes.” Prompt the child to stop you when you make a mistake. Then ask what the mistake was. For example, if you say, “1, 2, 3, 3, …” the child might explain that you said 3 twice. Watch Ben: Catch My Mistake here.

• Matching objects with one to one correspondence  Present a small number of tallies, such as 2 tallies. Point to the tallies and ask the child to show that many objects. You can also ask count out small numbers of toys and ask the child to match counters, one by one, to the toys.  Watch Ben: Matching Tallies to Counters here.
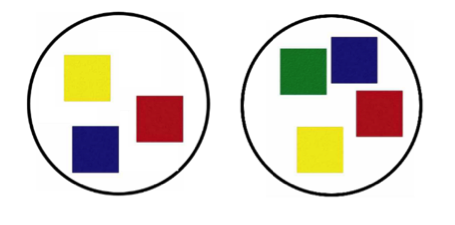• Identify sets that show specific numbers  See if the child can recognize numbers. For example, place 3 tiles on one plate and 4 tiles on another. Ask, “Can you point to the plate that has 3 tiles?” See if the child can do this without counting.
• How many are there? Present a set of objects and ask, “How many?” For a younger child, give a small number of objects. For an older child, give a larger set. Pay attention to how the child counts and any strategies used. For example, does she just say the number without touching or pointing to them? Does she count them in a clump, possibly count some objects twice or missing some objects? Does she move each object to the side to make sure she counts each object once and exactly once?  After counting, ask the child, “So, how many is that?” This will give you good information about whether the child understands cardinality—the total number of the set. If the child responds by recounting each object instead of repeating the total number, the child may not yet realize that the number obtained from the initial count still applies and counting again is not necessary.
• Can the child produce an amount?  Present a container or pile of objects, such as bears. Ask, “Can you give me 6 bears?” See if the child is able to keep track, counting out only 6 bears. For older children, ask for greater numbers of objects, but do not ask for all of the available objects.

• Conservation of number  After a child has counted a set of objects, hide them under a cover or move them in a different arrangement. Ask, “How many are there now? How do you know?”  See if the child says that whatever the number, mere physical re-arrangment (without adding or taking away anything) does not change it.  Watch Meredith: How Many Bears? here.
• Conservation of equivalence   Place a row of objects in front of the child, such as 5 counters. Say, “There are your counters.” Then place another row of 5 counters lined up with the first row (see top half of figure). Say, “There are my counters.” Ask the child to count how many counters you each have. Then 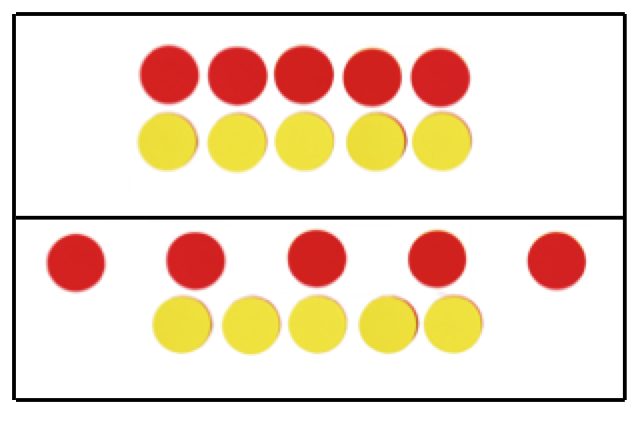say, “Do I have more, do you have more, or do we have the same number?” If the child says they are the same (meaning that the two numbers are equivalent), say, “Okay, now watch what I do.” Spread out one of the rows of counters so there are still 5, but now that one row is further apart (see bottom half of figure). Ask, “How about now? Do I have more, do you have more, or do we have the same number?” If the child says that the more spread out row is more numerous, ask the child to count again. If the child says each row still has 5, ask again which has more. If the child says the longer row is still more numerous, the child is not conserving equivalence yet.  If the child knows both rows are still the same in number, even when one is spread out, the child is conserving equivalence.