with commentary by Herbert P. Ginsburg

Catherine Rau was a student in my course, the Development of Mathematical Thinking. One assignment was to conduct a clinical interview exploring a young child’s mathematical knowledge, to use the results of this formative assessment to guide teaching, and to write up the whole experience. Catherine chose to focus on the understanding of shape. Her interview, her teaching, and her write-up were all so interesting that I thought other students—you—could benefit from reading her paper and viewing the embedded video clips.  

Here is a very lightly edited version of Catherine’s paper, along with the video clips of her interaction with Sawyer. At various points, you'll see my comments in purple italics. Her paper begins with an introduction.

Introduction

Young children come to recognize, categorize, and refine their ideas of geometric shape every day. They take notice of the shapes of their beds, their cereal bowls, and the wheels of their scooters. The bottom line is, geometric shapes are all around us. And it is important for young children to be exposed to geometric shapes not only inadvertently but also “advertently.” This is where teachers come in. Recognizing what children already know about shapes (through observation or clinical interview), it is important for teachers to build on such information and ideas in order to authentically refine children's ideas of shape.

Goals and Background Literature

The assessment that I conducted with Sawyer was aimed to gauge his initial knowledge of shapes, without providing significant help or guidance though scaffolding or teaching. I started off by setting out paper cutouts of prototypical shapes (triangle, square, rectangle, circle), asking him to hand me each shape one by one as I stated their names. This exercise tests Sawyer's discrimination skills. This differentiation skill is key in figuring out young children's understanding of shape.

Catherine began with a statement of her goals. It is important to recognize that the clinical interviewer usually has clear goals in mind, along with specific tasks to use in the interview. Catherine went on to describe other interview goals, the tasks to be used in the interview, and theoretical relevance of the tasks. She also provided useful background. 

Background Information

For this assignment I chose to interview the same little boy, Sawyer (pseudonym), whom I interviewed for my midterm. At this time, Sawyer is now four years and five months old. He still attends preschool five days a week. Having done the clinical interview with Sawyer in October I figured it would be nice to also interview him for the final assignment (in December). But it wasn't until Sawyer approached me at school randomly, the other week, to ask when we would be doing math again together, that I knew I absolutely had to interview him. He told me that he really liked learning math with me and that he wanted to do more fun math games and for even longer this time. While his stomach may have been talking, remembering the sweet treats we used in doing the math activities, I couldn't help but smile and agree to do more math with him incorporating a different tasty treat into the activities.

As Catherine says, Sawyer may have been angling for the sweets, but we have worked with many children who clearly enjoy the interview process for its own sake. Why? One possibility is that the interview is one of the few occasions on which adults truly try to learn about the child’s thinking. The child is the focus of adult attention and stands in the limelight. Also, is it possible that a child can be interested in learning about her own thinking.

This time I expected the interview to take place in the hallway of the school, as it did, but it was not quiet. There were other teachers out and about, even some sitting a foot away from my space, which distracted Sawyer and me. Later, my lesson and follow up interview took place in the school director's office (as I was not expecting). With materials all over the place, this environment too distracted Sawyer. And as if those distractions weren't enough, Sawyer's teacher advised him to eat his snack during my lesson in order to save time; so I apologize for and hope you can bear with the many distractions and tangents that occurred in my interviews.  

Catherine’s experience is not atypical. Interviewers often have to operate in situations that are less than ideal. Nevertheless, judge for yourself whether the distractions spoil the interview. Also, be aware that as teachers, you will have to operate under similar conditions when you interview children in your classrooms.

Main Findings

At the beginning of the interview, I came to realize that Sawyer was able to distinguish prototypical shapes from each other based on their names and a few attributes.

Having a good grasp of basic shape discrimination, he was able to complete my first task. But his explanations of how he knew to classify certain shapes threw up a red flag. That is, Sawyer seemed to be missing much information. For example, it is correct to point out that a triangle has a pointy edge. However, if this is the only attribute of a triangle in Sawyer's mind, he is missing some pieces to the puzzle.

Trying to further gauge Sawyer's knowledge of triangles I introduced two non-prototypical triangles to him, one at a time. 

For the first triangle, Sawyer makes a connection between this shape and the 3D blocks in the block station. “We have one of these kind of blocks.” He also seems to be getting at its right triangle properties, explaining that it can “lean up against things.” However, when asked why it is a triangle, Sawyer again only verbalizes it is a triangle "…because it also has a pointy edge." With the introduction of the second triangle, which is not shown on the video, the same thing happens. Sawyer only identifies the triangle by regarding one of its corners to be pointy. He shows no mention of its straight lined sides, or its two other corners.

Notice several features of the interview. One is that Catherine listens to Sawyer’s comments and asks him to follow up on them. Thus, after he refers to the “special kind” of triangle, Catherine asks why it is special. A second is that Catherine asks probing questions in a kind and engaging manner. “But how did you know that is a triangle?” A third is an interesting event that I think Catherine missed, namely that Sawyer rotated the triangle as he was talking about it. He seemed to believe that this kind of transformation is irrelevant to a triangle’s defining characteristics. Because many young children do not understand this idea, it might have been interesting for Catherine to explore Sawyer’s understanding of the transformation and its effects. She continues.                                                                     

Attempting to get more out of Sawyer than his "pointy edge" definition I chose to show Sawyer an upside down heart, emphasizing its pointy edge, interested to see how he would classify it or if he would potentially verbalize more attributes of a triangle.

But rather than defending the shape as a heart or a triangle, Sawyer explained that it was both. It was a heart right side up; and it was a triangle because it had a pointy edge, but a special triangle because of its bottom.

I thought that maybe Sawyer explicitly indicated, by a movement of his finger, that the bottom was curved. Check it out. Catherine continues.

Sawyer's triangle schema seems to have a hole in it. He seemed unaware of a triangle's attribute of possessing three straight-lined sides. To learn more, I pressed Sawyer with the activity of identifying triangles on the triangle-esque filled worksheet shown here. 

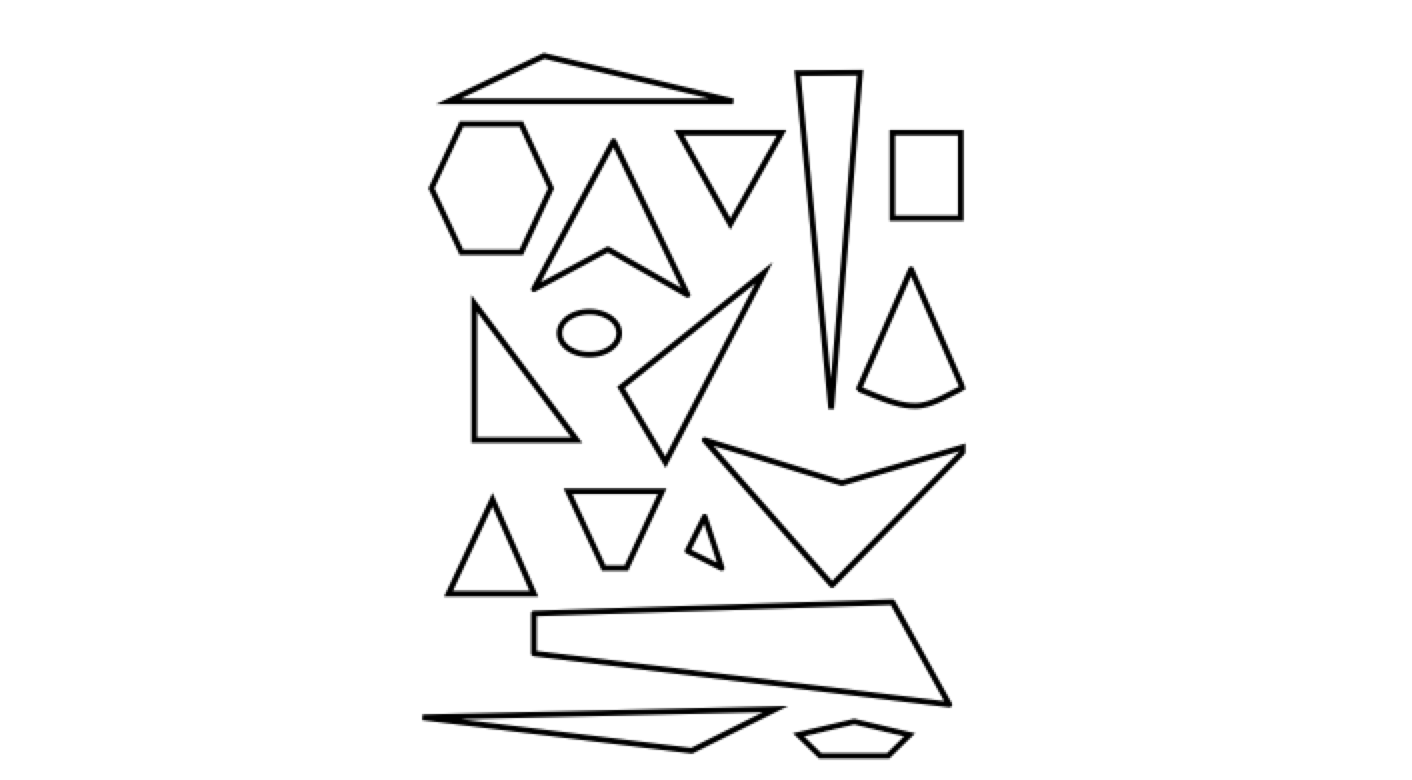
The interview continued.

I found that hole in his understanding to be bigger than expected. He identifies every shape on the worksheet to be a triangle, pointing out each shape's pointy edge. Again, the importance of children learning shape attributes as well as their names is shown in this instance. They need to learn why some figures are triangles and some not. The last triangle exercise I chose to do with Sawyer was for him to draw a triangle. I wanted to make sure that I was giving Sawyer enough opportunities to express his ideas and knowledge.

But as Sawyer struggled with drawing, Catherine wisely decided not to continue to walk down this particular avenue. Drawing can be a useful means to learn about a child's ideas, but apparently this was not the case for Sawyer.

Teaching

I decided that for my lesson I would teach Sawyer the attributes of a triangle. However, I would do so in a discovery type of manner. 

By allowing Sawyer to discover and feel the attributes of the triangles, with minimal guidance, I thought he would authentically understand and remember them better. When asked to think about his previous definition of triangles of having "one pointy edge," Sawyer is able to expand upon his previous idea by looking at the triangles in front of him to see that they have three "corners," not just "one pointy edge."

Notice that Catherine spent some time encouraging Sawyer to feel the triangles. The unstated assumption is that several senses, not only vision, can contribute to learning. Feeling the triangles provides a kind of bodily substance to the mathematical concept. The feeling (including a painful one) generated by touching the “pointy edges” may contribute to the idea of a vertex. 

By inviting Sawyer to think about other possible attributes of triangles he is able to discover them on his own.

Noticing that the triangles are all flat (which “everybody knows”), Sawyer raises the point that the shapes in front of him are two-dimensional. This is a very astute observation from a four year old. Sawyer also sees that there are three long lines that come together at the corners. His change in tone when saying this, to me, indicates that he has discovered something he hadn't realized before. Or at least by visually and physically tracing the triangle, Sawyer had reinforced an idea he may have previously had about triangles, making it click in his mind.

I’m not sure about Catherine’s interpretation of the change in tone.  Maybe she was skeptical as well, because she added an alternative hypothesis about reinforcement of a previous idea. One characteristic of sound interpretation is the ability to be aware of the limitations of a hypothesis and to develop alternative explanations. 

Not wanting Sawyer to get the idea that all the lines of a triangle had to be long I asked him if it was okay to have a shorter line as well.

While his explanation wasn't the most clear to me, he seemed to understand that the length of the lines was not an issue.

Sawyer certainly stressed the idea of medium. I wonder though if he would accept a line extremely longer than those he sees on the triangles. Catherine continued.

However, when I invited Sawyer to look at the lines of the triangles, he noticed another attribute. 

That is, Sawyer noticed that triangles have three straight lines and showed his further understanding pointing out that they aren't “zig, zag lines.” 

After guiding Sawyer to those discoveries one by one, he was then able to tell me the three important properties of triangles.

Hearing him list those properties of triangles made me confident that his definition of a triangle was definitely expanded from “having one pointy edge.” 

Did you notice, dear reader, that Catherine seems to be writing backwards, from right to left? She’s not. The video recording somehow “flipped” her around, which is an interesting kind of transformation, but not one we will discuss here.

In terms of the follow-up exercises that I did with Sawyer, I purposely chose to do the same ones that I used in his pre-assessment in order to compare the results, prior to and after the lesson.

Sawyer gets off to a bit of a rocky start. He is less focused on the task than on getting his stuffed animal raccoon. But after I remind him to focus, he seems to snap back into it.

In this clip we see Sawyer thinking and concentrating to correctly circle all shapes that have three corners and three straight lines, identifying some as not triangles in the process. This identification and ability to pick out triangles among distractor shapes is very important in showcasing Sawyer's true understanding of the properties of a triangle. And it too shows Sawyer's progress going from marking every shape on the page to being able to distinguish among the shapes on the worksheet.

Conclusions

Overall, despite countless distractions from the environments of the interviews, Sawyer's snack eating, and his new stuffed animal raccoon he got for animal day, I think my interviews and lesson with Sawyer went relatively well. While Sawyer was not able to perfectly complete each task, he showed definite progress in his mathematical thinking of triangles from the pre-assessment to the post assessment. And by learning to discriminate/identify triangles using his newly learned knowledge of their attributes, Sawyer showed thorough understanding and transfer from the lesson to the post assessment. With this being one of the few lessons I have ever taught to a child, let alone math lessons, it was inspiring to see Sawyer really learning, interacting with, and enjoying the math activities that I was doing with him.

Conducting this three-pronged assignment with Sawyer emphasized just how important it is to pay attention to children's math for more than just surface learning. For example, had I assumed Sawyer knew his shapes based on his ability to name them on the playground, I would not have discovered the holes in his ideas and definitions of triangles. It is no secret that math is not everyone's favorite subject to teach or to learn, but taking the time to set up rich and meaningful math lessons for children may be a means to detract from negative feelings around early childhood mathematics. While I would love to keep working with Sawyer uncovering more and more of the mathematical thinking going on in his four-year-old head, and while I'm sure he would love to do the same, it makes me happy to know that Sawyer's first few structured, mathematical experiences in his young life have been positive, educational, fun, and most of all memorable.

And my conclusion is that I hope Catherine’s video essay helped you understand children’s concepts of shape ideas and also sound methods of interviewing, interpreting, and intentional teaching. Kudos to Catherine and Sawyer.