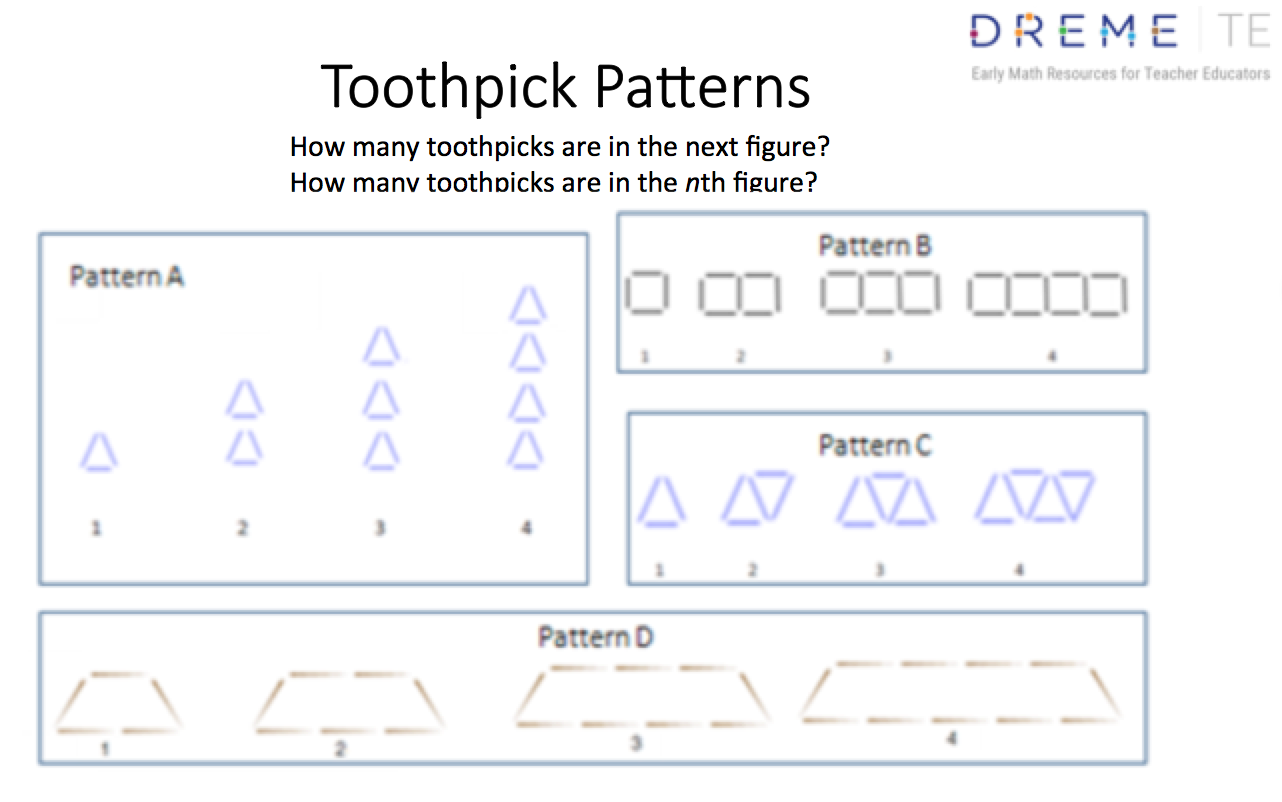
What do we mean by pattern? Can young children engage in algebraic thinking to understand patterns? How should we help young children to think about and understand patterns?
REGULARITY, REGULARITY, EVERYWHERE
Young children, even babies, are exposed to many, many regularities in their worlds and in themselves. They encounter regularities that are fixed and do not move, like stripes on clothing. Other regularities unfold over time, like songs, or continue indefinitely, like counting by twos.
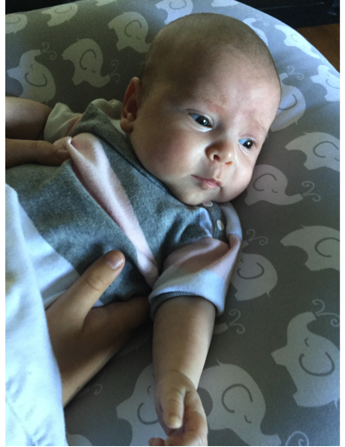 Babies: One type of regularity involves visual patterns in the immediate environment which are available for babies to see and examine. Indeed, research shows that babies prefer to look at patterns, rather than at uniform scenes, perhaps because patterns provide opportunities to discern differences. Baby Cassie might discern the beautiful patterns on her Boppy (a pillow on which she can recline). The elephants are evenly spaced in lines and rows, the elephant’s ears are roughly in the middle of each body, and out of each of the trunks spouts a horn-shaped stream of water.
Babies: One type of regularity involves visual patterns in the immediate environment which are available for babies to see and examine. Indeed, research shows that babies prefer to look at patterns, rather than at uniform scenes, perhaps because patterns provide opportunities to discern differences. Baby Cassie might discern the beautiful patterns on her Boppy (a pillow on which she can recline). The elephants are evenly spaced in lines and rows, the elephant’s ears are roughly in the middle of each body, and out of each of the trunks spouts a horn-shaped stream of water.
Cassie will also hear regularities in music, in the repeating sequences of sounds. Her parents will sing tunes such as “Hush little baby, don’t say a word, Papa’s gonna buy you a mocking bird,” and “There was a farmer had a dog, and Bingo was his name, oh. B-I-N-G-O…” Maybe she will even hear her mother’s steady heart beat during nursing.
The environment provides a wealth of regularities from which babies may (or may not) extract pattern and other information.
 Preschoolers: By the time children are in preschool, they have experienced an incredibly large number of regularities. Some involve spatial relations and shapes, as is the case in this picture of Rabbit’s home in a preschool classroom. A child in this classroom could see the regular, orderly rows and columns of rectangles, each with height approximately double the base; the ramp divided into approximate squares, separated by “lines” (thin rectangles of wood), and ascending at about a 45° angle to the floor. The steps, which are all the same, ascend in a regular pattern. In the background, the green rectangular buckets (prisms) are stacked neatly on top one another, each rising a constant amount over the others, until this pattern is crowned in purple. Of course, children would not describe these regularities in such adult terms. But the regularities pervade the child’s quotidian environment and set the stage for learning about shapes, patterns, and much else.
Preschoolers: By the time children are in preschool, they have experienced an incredibly large number of regularities. Some involve spatial relations and shapes, as is the case in this picture of Rabbit’s home in a preschool classroom. A child in this classroom could see the regular, orderly rows and columns of rectangles, each with height approximately double the base; the ramp divided into approximate squares, separated by “lines” (thin rectangles of wood), and ascending at about a 45° angle to the floor. The steps, which are all the same, ascend in a regular pattern. In the background, the green rectangular buckets (prisms) are stacked neatly on top one another, each rising a constant amount over the others, until this pattern is crowned in purple. Of course, children would not describe these regularities in such adult terms. But the regularities pervade the child’s quotidian environment and set the stage for learning about shapes, patterns, and much else.
Learning language also involves many regularities: English plurals of nouns mostly have an s at the end but individual nouns do not; for example, birds and bird, or bees and bee. There are few exceptions to the rule, as in the case of child and children. English indicates the past tense by adding ed to verbs: “I kicked the ball.” Again, there are exceptions as in “I found the ball,” instead of “I finded the ball.” Young children clearly notice the regularities, as is evident from some of their mistakes, like, “I goed to the store where I finded the mooses.” Indeed, the mistakes are evidence that the childrens (I’m working on my plurals) noted the regularities and used them to form a rule which they overgeneralized.
DYNAMIC AND STATIC PATTERNS
We use the word pattern to refer to some (but not all) regularities. Pattern is a very complex and general term, like understanding. In early math education, we tend to focus on two broad types of patterns: dynamic and static. We might say that dynamic patterns are going somewhere, but static patterns are happy where they are. Dynamic patterns, like a song, unfold over time. A dynamic alternating pattern can in principle extend indefinitely. By contrast, static patterns, like stripes on a dress, are complete in themselves. Looking at the dress, you can see all the stripes, the full pattern, and there are no more stripes, nothing more to see.
UNDERSTANDING PATTERN
The goal of early math education should be to help children deepen and mathematize their understanding of pattern. They need not only to perceive the pattern on the dress, but also to describe it in explicit terms. In the most general sense, children need to focus on the structures and rules that underlie overt surface phenomena (just as the linguist attempts to uncover the grammatical rules that underlie speech). If children understand patterns, they will be able to describe them, reproduce them, extend them, fill in missing elements, and create new patterns. Preschoolers can learn much more than a rote recitation of ABAB patterns, which is of limited importance in early math education.
WHAT PATTERNS SHOULD YOUNG CHILDREN STUDY?
Children should learn about a variety of patterns, both static and dynamic. These include:
-
alternating patterns, including
-
the shapes: circle-square-circle-square…
-
the colors: red-blue-blue-red-blue-blue…
-
the musical sounds: do-do-re-re…,
-
-
growing patterns, for example, the increasing height of block towers,
-
number patterns such as skip counting, grouping by tens, and simple number tables (like the hundreds chart, which can contain a great deal of rich mathematics),
-
equivalence of patterns, for example the equivalence between an alternating-colors pattern and a pattern of alternating shapes or even sounds,
-
musical patterns such as ascending and descending melodies,
-
spatial relations, like the symmetries involved in block constructions,
-
and methods for representing patterns: by drawings or symbols (like A and B) and eventually the written symbolism that is at the heart of algebra.
HOW SHOULD WE TEACH PATTERNS?
One approach is to seize upon teachable moments that arise in the everyday environment. For example, the constructions that children create in their artwork and block play often contain patterns. The teacher can ask children to describe their creations and perhaps even talk about how the constructions involve patterns. “Tell me about what you did with these blocks. Why did you put these over here and the other ones over here? Do you see a pattern? Why do you think it’s a pattern?”
Another approach is guided instruction, in which the teacher uses various manipulatives or other tools (a piano or the voice, or paper and crayon, or digital devices) to systematically develop various ideas about pattern. “Let’s use these blocks to make a staircase.” “Try to make this part of the house the same as that part.”
Regardless of the specific content, manipulatives, and tools used, teachers should emphasize thinking and communicating about patterns and the structures underlying them. The use of standard written symbols is usually not appropriate for children at this age level, but describing, communicating, and thinking are essential from the outset.
Therefore, no more, or perhaps only a light appetizer of: A B A B A B A B A B A B A B A B A B A B A B A B A B A B A B A B A B A B A B A B A B A B!
Download an Expanded Version of What Young Children Know and Need to Learn about Pattern and Algebraic Thinking below.