We describe a way to engage participants in learning about patterns and algebraic thinking in Teaching Algebraic Thinking to Young Children. Here is a description of how we used the activity as part of a university course.
Emma's Representation
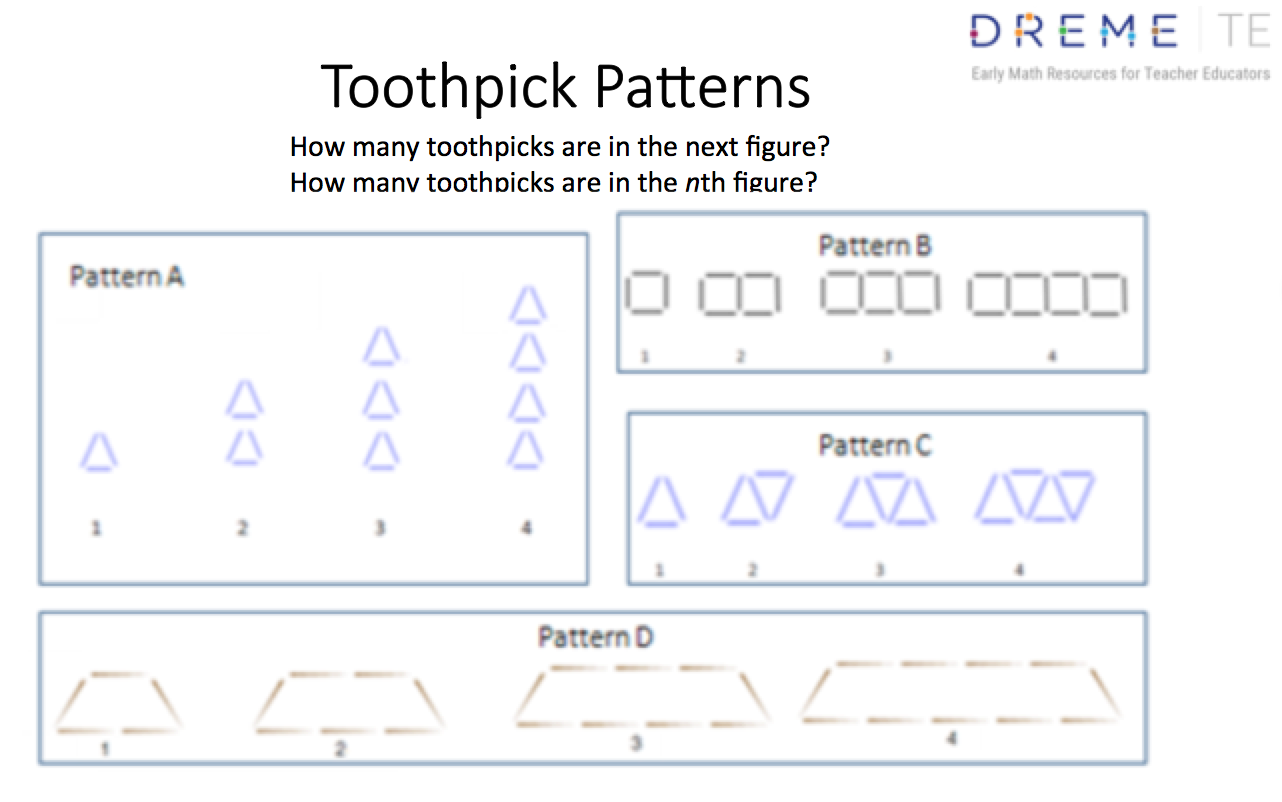
 We begin with the work of “Emma,” who explored Pattern A by drawing a three-toothpick triangle. She wrote an n inside it and labeled it 1. Then, above the 1st triangle, she drew another three-toothpick triangle, this time writing "+3" in the middle and labeling it 2. Finally, she drew another three-toothpick triangle, wrote "+3" inside, and labeled it 3. The meaning of these representations is not entirely clear. Does Emma mean n in the bottom triangle to represent the number of toothpicks? Then what about the two triangles above the bottom triangle? She wrote "+3" inside each. Does this mean that the triangles they represent have the same number of toothpicks or that 3 toothpicks are added to the previous triangle to get the next triangle in the figure? Emma's drawings are an attempt to capture a valid recursive rule: add 3 more toothpicks to each triangle to get the next triangle. While imperfect, the drawings did allow her to explore Pattern A.
We begin with the work of “Emma,” who explored Pattern A by drawing a three-toothpick triangle. She wrote an n inside it and labeled it 1. Then, above the 1st triangle, she drew another three-toothpick triangle, this time writing "+3" in the middle and labeling it 2. Finally, she drew another three-toothpick triangle, wrote "+3" inside, and labeled it 3. The meaning of these representations is not entirely clear. Does Emma mean n in the bottom triangle to represent the number of toothpicks? Then what about the two triangles above the bottom triangle? She wrote "+3" inside each. Does this mean that the triangles they represent have the same number of toothpicks or that 3 toothpicks are added to the previous triangle to get the next triangle in the figure? Emma's drawings are an attempt to capture a valid recursive rule: add 3 more toothpicks to each triangle to get the next triangle. While imperfect, the drawings did allow her to explore Pattern A.
Jade's Representation
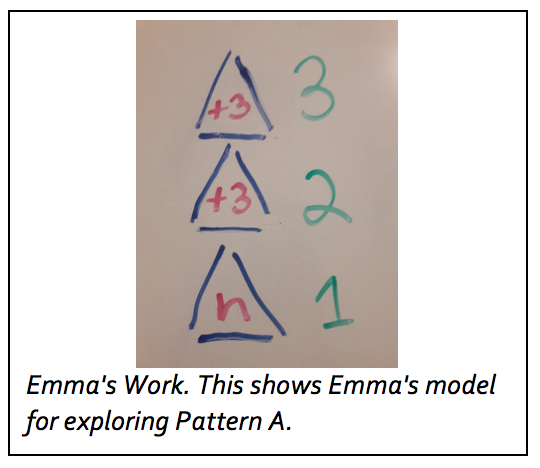
Let's contrast Emma's model with Jade’s more advanced representations. She also determined that 3 toothpicks are added each time in Pattern A, but represented the pattern in a horizontal table. In the top row, she wrote the numbers 1, 2, 3, and 4 to show the position of each figure in the pattern (1st, 2nd, 3rd, and 4th). She then wrote the number of toothpicks in each triangle in the second row. She used this same model for Pattern B. By comparing the values in the second rows of each pattern (that is, the 3, 6, 9, and 12 vs. the 4, 7, 10, and 13), she was also able to determine that in both patterns, 3 toothpicks are added to create the next triangle or square.
Emma's representation hinted imperfectly at a recursive rule while Jade's allowed her to find the rule and show it accurately. However, neither student developed an algebraic rule for finding the nth figure in each pattern (which was the second question posed). But as, mentioned earlier, the goal of this activity is not for students to know right away how to symbolically represent the rules, but rather to give them a chance to explore and discover the rules.
Representing Vertically
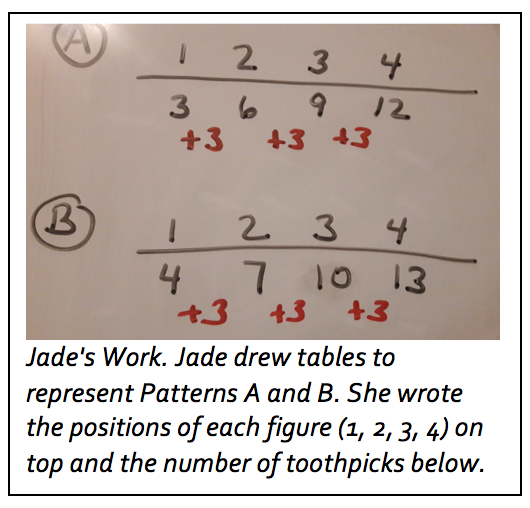
The challenge for students like Emma and Jade seemed to be that the recursive rule involves adding 3, but the algebraic rule involves multiplying the position number, n, by 3. For example, column 2 in Pattern A is made up of 2 triangles each with 3 toothpicks, so the total number of toothpicks is equal to 3 + 3 or 3 x 2. The total number of toothpicks in figure 3 is equal to 3 + 3 + 3 or 3 x 3. The total number of toothpicks in figure 4 is equal to 3 + 3 + 3 + 3 or 3 x 4. To help students acquire this algebraic insight, the course assistant suggested to a pair of students, Anju and Marlena, that they represent Pattern A in a vertical table. They labeled the first column n, the position of the figure, and the  second column t, the number of toothpicks in the figure. She then asked them to make a third column and list the numbers of toothpicks for Pattern B right beside those for Pattern A. Looking at this table, Anju and Marlena noticed that the number of toothpicks for each figure in Pattern A is 3 times the value of n (the position of the figure). They wrote t = 3n, which is the algebraic rule for Pattern A. This representation greatly helped the students recognize this relationship.
second column t, the number of toothpicks in the figure. She then asked them to make a third column and list the numbers of toothpicks for Pattern B right beside those for Pattern A. Looking at this table, Anju and Marlena noticed that the number of toothpicks for each figure in Pattern A is 3 times the value of n (the position of the figure). They wrote t = 3n, which is the algebraic rule for Pattern A. This representation greatly helped the students recognize this relationship.
Finding the algebraic rule for Pattern B is less obvious, however, using just a vertical table, which is why the instructors suggested they place the two patterns side by side as shown. As Picture 3 shows, Marlena and Anju compared the numbers of toothpicks in Pattern A to the numbers of toothpicks in Pattern B and noticed that the values for Pattern B were all 1 more than the corresponding values for Pattern A. This helped Anju and Marlena achieve an algebraic insight. They realized that they could add 1 to the algebraic rule for Pattern A to find the algebraic rule for Pattern B. Therefore, the algebraic rule for Pattern A is 3n. So, the algebraic rule for Pattern B is 3n + 1.
Reflection
After reflecting on the activity, some students reported that it reminded them of “high school algebra” while others experienced it as a “fun ‘crack the code’ activity.” Even though Marlena and Anju were both successful, Marlena reflected, “I was a bit discouraged because my group was getting the answers rather fast, and I wasn't.” Anju on the other hand, wrote, “Although it was challenging and took us a while to figure out the algebraic formula for the nth term, it was an extremely fun process, and I felt really excited when we finally figured them out! Once the course assistant showed us the tabular method of representing the pattern, we had an ‘ah ha!’ moment, and I felt immense satisfaction at being able to solve the rest of the patterns. It just shows that once something clicks for a student, so that she understands a method, she will be open to and may enjoy solving many more such problems.”